[알고리즘] 탐색 알고리즘, 정렬 알고리즘 정리(javascript)

알고리즘

주어진 문제를 해결하기 위한 절차나 규칙의 집합입니다. 컴퓨터 과학에서 알고리즘은 입력(input)을 받아 출력(output)을 생성하기 위한 단계적인 계산 과정을 설명하는 명확하고 명백한 절차입니다. 알고리즘은 문제 해결의 지침을 제공하며, 정확하고 효율적인 결과를 얻기 위해 따라야 할 단계들로 구성됩니다.

 

알고리즘 특징

정확성: 알고리즘은 주어진 문제를 정확하게 해결해야 합니다.
효율성: 알고리즘은 가능한 한 효율적으로 동작해야 합니다. 실행 시간, 메모리 사용량 등을 최적화하여 최고의 성능을 달성해야 합니다.
일반성: 알고리즘은 주어진 문제에 대해 모든 입력에 대해 동작해야 합니다. 특정 조건이나 입력에 특화된 알고리즘은 제한적인 활용성을 가질 수 있습니다.
확장성: 알고리즘은 입력 크기에 따라 적절하게 확장될 수 있어야 합니다. 큰 입력에 대해서도 효율적으로 동작할 수 있어야 합니다.

 

탐색 알고리즘

탐색 알고리즘은 주어진 데이터 집합에서 특정 항목을 찾는 과정을 나타내는 알고리즘입니다. 데이터 집합은 배열, 리스트, 트리 등의 자료 구조로 표현될 수 있습니다. 탐색 알고리즘은 효율적으로 원하는 항목을 찾기 위해 데이터를 조사하고 탐색하는 방법을 정의합니다.

 

선형 탐색 알고리즘 (Linear Search)

- 맨 앞이나 맨 뒤부터 순서대로 하나하나 찾아보는 알고리즘
- 순서 : 맨 끝부터 순서대로 탐색 → 원하는 값을 찾으면 탐색 종료
- 5를 찾을 때, 맨 왼쪽에 있는 1부터 시작해서 하나씩 탐색

// 다음은 배열의 요소중 5인 index를 찾아보는 함수입니다.
// 선형 탐색법에 대한 공부중이기에 명확해보이는 함수로 작성해보겠습니다.

function findIndexLinear(array, condition) {
  for (let i=0; i<array.length; i++) {
    if (array[i] === condition) {
      return i
    }
  }
}

// 최선의 경우 - 한번의 탐색으로 해결
findIndexLinear([2,4,5,1,6], 2)
// 최악의 경우 - 배열의 크기만큼 탐색으로 해결
findIndexLinear([2,4,5,1,6], 6)

 

 

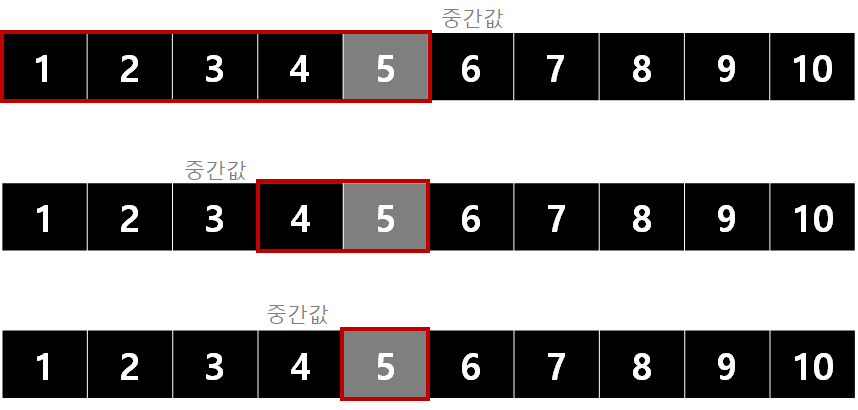
이진 탐색 알고리즘 (Binary Search)

- 중간지점을 기준으로 데이터를 반씩 나눠서 탐색하는 알고리즘
- 순서 : 가운데 요소 먼저 탐색 → 조건이 가운데 요소보다 정렬순서가 빠른지 느린지 보고 탐색 범위 좁힘 → 탐색 범위를 좁혔으면 다시 가운데 탐색 → 반복
- 선형탐색은 n이 증가함에 따라 시간복잡도가 선형적으로 증가하지만, 이진탐색은 n이 증가해도 시간복잡도가 아주 천천히 증가
- 보통 정렬된 리스트에는 이진탐색을 사용하고, 정렬되지 않은 리스트에는 선형탐색을 사용
- 5를 찾을 때

function findIndexBinary(array, condition) {
    let head = 0;
    let tail = array.length - 1
    // 아래와 같이 배열의 크기가 짝수인 경우에는 3가지 옵션이 있습니다.
    // 1. 반올림 (Round)
    // 2. 올림 (Ceil)
    // 3. 내림 (Floor)
    // 이번에는 내림을 이용하여 구현을 해보겠습니다.
    let centerIndex  = Math.floor((head + tail) / 2) // 2.5
    
    while(array[centerIndex] !== condition) {
        // 찾는 결과가 없을 떄 (infinity loop prevent)
        if(head > tail) return '결과를 찾지 못했습니다.'

        if (array[centerIndex] < condition) {
          head = centerIndex + 1;
          centerIndex = Math.floor((head + tail) / 2)
        } else {
          tail = centerIndex - 1;
          centerIndex = Math.floor((head + tail) / 2)
        }
    }

    return `${centerIndex}번째 요소가 일치`
}


findIndexBinary([1,2,4,5,6,7], 7)

 

 

해시 탐색 알고리즘 (Hash Search)

- 값과 index를 미리 연결해 둠으로써 짧은 시간에 탐색할 수 있는 알고리즘
- 해시 탐색을 위해서는 데이터를 저장하는 알고리즘과 데이터를 검색하는 알고리즘 필요
- 해시함수를 사용하여 데이터를 저장하는 알고리즘 :

// 먼저 배열을 2개 준비합니다.

let arrayA = [12,25,36,20,30,8,42]

// 앞에서 배운 2개의 검색 알고리즘(선형 탐색, 이진 탐색)은
// 배열의 요소를 데이터 수만큼 준비하면 충분했지만,
// 해시 탐색법은 이와 달리 저장하는 데이터의 1.5~2배를 준비해야 합니다.
let arrayB = new Array(11).fill(0)

// 저장할 요소의 배열을 순회하면서
for (let i=0; i<arrayA.length; i++) {
  // 저장할 공간(첨자)를 계산
  let temp = arrayA[i]%11;
  // 저장할 공간에 데이터가 없으면
  if (!arrayB[temp]) {
    // 저장합니다.
    arrayB[temp] = arrayA[i]
    // 저장할 공간에 데이터가 있으면
  } else {
    // 데이터가 없는 공간을 찾을때까지
    while(arrayB[temp]) {
      // temp를 증가, 하지만 배열의 크기가 11이므로, 
      // 인덱스가 10을 넘으면(배열의 크기를 넘으면 안되기에) 0으로 변경합니다.
      temp < arrayB.length-1 ? temp++ : temp = 0
    }
    // 데이터가 없는 공간을 찾으면 저장합니다.
    arrayB[temp] = arrayA[i]
  }
}

// [ 42, 12, 0, 25, 36, 0, 0, 0, 30, 20, 8 ]

- 저장된 데이터를 탐색하는 알고리즘

// 저장한 데이터와 찾을 요소를 Argument로 넣어줍니다.
function findHashData(arr, target) {
  // 저장할 공간에 데이터가 있어서 +1해준 경우를 제외하고는
  // 첨자 = 저장할데이터 % 저장할 배열의 크기입니다..
  let uniqueValue = target%arr.length;

  // 찾고자 하는 값이 맞을 경우가 나올때까지
  while (arr[uniqueValue] !== target) {
    // 결과가 원하는 값이 아니면, (저장할데이터+1) % 저장할 배열의 크기
    uniqueValue = (uniqueValue+1)%arr.length
  }
  return `저장 위치는 ${uniqueValue}번째 요소입니다.`
}

findHashData(arrayB, 42)
// => '저장 위치는 1번째 요소입니다.'

- 구현은 기존 탐색법보다 어렵지만 검색 알고리즘 중에서도 매우 속도가 빠른 알고리즘

 

 

너비 우선 탐색 알고리즘 (BFS, Breadth-First-Search)

- Node 같은 레벨에 있는 Node들 (형제 Node들)을 먼저 탐색하는 방식
- BFS 순서: A - B - C - D - G - H - I - E - F - J

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"]
};

const BFS = (graph, startNode) => {
  const visited = []; // 탐색을 마친 노드들
  let needVisit = []; // 탐색해야할 노드들

  needVisit.push(startNode); // 노드 탐색 시작

  while (needVisit.length !== 0) { // 탐색해야할 노드가 남아있다면
    const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
    if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
      visited.push(node); 
      needVisit = [...needVisit, ...graph[node]];
    }
  }
  return visited;
};

console.log(BFS(graph, "A"));
// ["A", "B", "C", "D", "G", "H", "I", "E", "F", "J"]

 

 

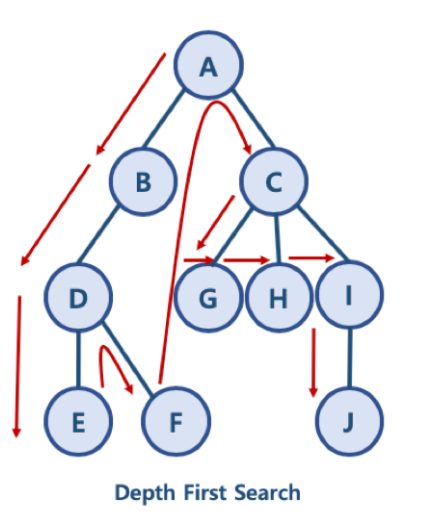
깊이 우선 탐색 알고리즘 (DFS, Depth-First-Search)

- Node의 Child들을 먼저 탐색하는 방식
- DFS 순서: A - B - D - E - F - C - G - H - I - J

const graph = {
  A: ["B", "C"],
  B: ["A", "D"],
  C: ["A", "G", "H", "I"],
  D: ["B", "E", "F"],
  E: ["D"],
  F: ["D"],
  G: ["C"],
  H: ["C"],
  I: ["C", "J"],
  J: ["I"]
};

const DFS = (graph, startNode) => {
  const visited = []; // 탐색을 마친 노드들
  let needVisit = []; // 탐색해야할 노드들

  needVisit.push(startNode); // 노드 탐색 시작

  while (needVisit.length !== 0) { // 탐색해야할 노드가 남아있다면
    const node = needVisit.shift(); // queue이기 때문에 선입선출, shift()를 사용한다.
    if (!visited.includes(node)) { // 해당 노드가 탐색된 적 없다면
      visited.push(node); 
      needVisit = [...graph[node], ...needVisit];
    }
  }
  return visited;
};

console.log(DFS(graph, "A"));
// ["A", "B", "D", "E", "F", "C", "G", "H", "I", "J"]

 

 

정렬 알고리즘

정렬 알고리즘은 주어진 데이터를 일정한 기준에 따라 오름차순 또는 내림차순으로 정렬하는 알고리즘입니다. 정렬은 데이터를 구조적으로 정리하여 검색, 비교, 분석 등 다양한 작업을 용이하게 하기 위해 중요한 작업입니다.

 

버블 정렬 (Bubble Sort)

- 첫번째 원소부터 인접한 원소와 비교하며 자리를 바꾸면서 맨 끝부터 정렬하는 방식
- 가장 큰값을 하나씩 뒤로 보내면서 뒤쪽부터 정렬하는 것
- 장점 : 구현이 간단, Stable 정렬(구현방식이 달라도 결과가 같음)
- 단점 : 시간 복잡도가 최악, 비효율적

function bubbleSort(arr) {
  for (let x = 0; x < arr.length; x++) {
    for (let y = 1; y < arr.length - x; y++) {
      if (arr[y - 1] > arr[y]) {
        [arr[y - 1], arr[y]] = [arr[y], arr[y - 1]];
      }
    }
  }
  return arr;
}

 

 

선택 정렬 (Selection Sort)

- 주어진 데이터 중 최소 값을 찾아서 해당 데이터의 맨 앞에 위치한 값과 교체 → 1회 진행할때마다 맨 앞쪽에 교체한 값은 제외, 그 다음 데이터도 차례대로 동일한 방법으로 교체
- 장점 : 구현이 간단, 비교 횟수에 비해 교환 횟수가 적음
- 단점 : 데이터를 하나씩 비교하여 비효율적, Unstable정렬(구현방식에 따라 결과가 다름)

function selectionSort(arr) {
  let indexMin;
  for (let x = 0; x < arr.length - 1; x++) {
    indexMin = x;
    for (let y = x + 1; y < arr.length; y++) {
      if (arr[y] < arr[indexMin]) {
        indexMin = y;
      }
    }
    [arr[x], arr[indexMin]] = [arr[indexMin], arr[x]];
  }
  return arr;
}

 

 

삽입 정렬 (Inseretion Sort)

- 버블 정렬의 비효울성 개선을 위해 등장
- i-1번째 원소까지는 모두 정렬된 상태여야 하며 i-1번째부터 0번째까지의 원소와 i번째 원소를 각각 비교 → i번째 원소보다 작은 값이 발견되면 그 위치에 i번째 원소 삽입 → 반복
- 장점 : 기존 배열 원소가 정렬되어 있을수록 속도가 빠름, Stable 정렬
- 단점 : 배열이 길어질수록 비효율적

function insertionSort(arr) {
  for (let x = 1; x < arr.length; x++) {
    let value = arr[x];
    let prev = x - 1;
    while (prev >= 0 && arr[prev] > value) {
      arr[prev + 1] = arr[prev];
      prev--;
    }
    arr[prev + 1] = value;
  }
  return arr;
}

 

---

기술면접이나 정보처리기사에 자주 나오는 문제들이여서 제가 주로 사용하는 언어인 javascript로 익히려고 노력했습니다.

 

요즘 정말 예습보다는 복습이 중요하다는 것을 느낍니다.